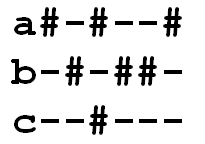exorciser.ch

Inhaltsverzeichnis

Aufgaben Serie C

Aufgaben Serie C

Loading ⌛Loading ⌛

1 X-Mas Tree

Erstelle einen Algorithmus der aus der folgenden Eingabe eine entsprechenden Weihnachtsbaum zeichnet:

Eingabe

ooooooo

Ausgabe

   o 
  ooo
 ooooo
ooooooo
   o

Die Grösse des Baumes ist abhängig von der Eingabe.
Erweiterung 1: Baumstrunk
Erweiterung 2: Baumschmuck

Loading ⌛

Lösung von Roli

/^(\s*)(o*)oo/ $1$2\n$&/
/^( *o)((\n *o*)*)$/$1$2\n$1/!

Lösung von Tscherter

/^( *oo?)\n[o\s]*/$&\n$1/!
/^( *o*)oo/ $1\n$&/

2 Pascalsche Dreieck

Erstelle einen Algorithmus der aus der folgenden Eingabe eine entsprechendes binäres Pascalsche Dreieck zeichnet.

Eingabe

oooooooooooooooooooooooooooooooooooooooo
o
o
o
o
o
o
o
o
o
o

Ausgabe

oooooooooooooooooooooooooooooooooooooooo
o o o o o o o o o o o o o o o o o o o o 
oo  oo  oo  oo  oo  oo  oo  oo  oo  oo  
o   o   o   o   o   o   o   o   o   o   
oooo    oooo    oooo    oooo    oooo    
o o     o o     o o     o o     o o     
oo      oo      oo      oo      oo      
o       o       o       o       o       
oooooooo        oooooooo        oooooooo
o o o o         o o o o         o o o o 
oo  oo          oo  oo          oo  oo

Loading ⌛

Lösung (TSC)

/αo([o \n]*)βo/oα$1oβ /
/αo([o \n]*)β /oα$1 βo/
/α ([o \n]*)βo/ α$1oβo/
/α ([o \n]*)β / α$1 β /
/α\no(.*)β(.)\no/\noα$1$2\nβo/
/α\n(.*)β(.)/\n$1$2/ !
/^o(o*)\no/oα$1\nβo/

3 Häufigste Wort in einem Text

Erstelle einen Algorithmus der jenes Wort aus einem Text herausliest, das am häufigsten vorkommt.

Eingabe

Allein sitzen, allein ruhen, allein gehen. Indem er sich selbst zaehmt, wird er gluecklich allein - allein im Wald.

Ausgabe

allein

Loading ⌛

Lösung

/\W+$//g
/ξ(\w+)\b(.*?)(ξ+)\1\b/ξ$3$1$2/g
/(ξ+)(ξ+)(\w+)\1(\w+)/$1$2$3/g
/.*ξ//!
/\W+|^/ξ/g

4 Zahlenreihe

Eine Zahlenreihe ist folgend aufgebaut: Man beginnt mit einer beliebigen Zahl.

Ist die Zahl gerade, kann sie durch zwei geteilt werden
Ist die Zahl ungerade, wird sie mit drei multipliziert und eins wird dazu addiert
Ist die Zahl 1 stoppt die Reihe

Beispiel: 6, 3, 10, 5, 16, 8, 4, 2, 1

Programmiere die Zahlenreihe als Markow Algorithmus für eine beliebige Eingabe in unärer Form. Beispiel:

Eingabe

Ausgabe

111
1111111111
11111
1111111111111111
11111111
1111
11
1

Loading ⌛

Lösung

/(^|\n)1$/$&/!              stopt bei 1
/(^|\n)(1+)\2$/$&\n$2/      halbiert die zeile
/(^|\n)(1+)$/$&\n$2$2$21/   verdreifacht die zeile +1

5 Römische Zahlen II

Schreibe einen Algorithmus der eine Dezimalzahl römisch darstellt. Bespiel:

Eingabe

Ausgabe

XXXXII

Loading ⌛

Lösung

/IIIII/V/g
/VV/X/g
/XXXXX/L/g
/LL/C/g
/CCCCC/D/g
/DD/M/g
/^α(.*)β//!
/9α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1$1$1$1$1$1/
/8α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1$1$1$1$1/
/7α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1$1$1$1/
/6α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1$1$1/
/5α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1$1/
/4α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1$1/
/3α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1$1/
/2α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1$1/
/1α(.*)β/α$1$1$1$1$1$1$1$1$1$1β$1/
/0α(.*)β/α$1$1$1$1$1$1$1$1$1$1β/
/$/αIβ/

6 Römische Zahlen III

Schreibe einen Algorithmus der zwei römische Zahlen addiert. Bespiel:

Eingabe

LIII + CLXIII

Ausgabe

CCXVI

Loading ⌛

Lösung

- Filtern
/[^MDCLXVI]//g
- Sortieren
/(I)([MDCLXV])/$2$1/g
/(V)([MDCLX])/$2$1/g
/(X)([MDCL])/$2$1/g
/(L)([MDC])/$2$1/g
/(C)([MD])/$2$1/g
/(D)(M)/$2$1/g
- Verdichten
/I{5}/V/
/V{2}/X/
/X{5}/L/
/L{2}/C/
/C{5}/D/
/D{2}/M/

Bemerkung: Der Algrithmus prüft nicht ob eine syntaktisch korrekte Addition vorliegt. Er addiert lediglich sämtliche vorhandene Zahlensymbole M, D, C, L, X, V und I zu einer einzigen römischen Zahl.

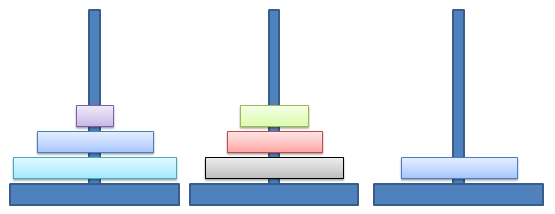
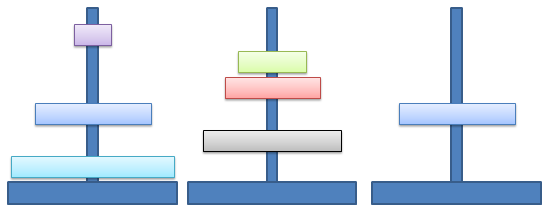
7 Towers of Hanoi

cf. Türme von Hanoi

Wir haben Scheiben, der Markow-Algorithmus arbeitet aber mit Buchstaben. Um die Lage der Scheiben zu beschreiben, braucht es eine geeignete Codierung:

Loading ⌛

Lösungen

Lösung von Sandro Ackermann

/α(.*)#([-]+)([bc].*)-\2(c|$)/$1-$2$3#$2$4/
/^(a.*)#([bc][#-]+)-(c|$)/α$1-$2#$3/
/^(a.*)-(b[#-]+-c)([#-]+)#/α$1#$2$3-/
/α(.*)-([-]+)([bc].*)#\2(c|$)/$1#$2$3-$2$4/
/α//!

Lösung von Vincent Tscherter

/ξ(\w.*)(\w.*)#(-+)(\w.*)-\3$/$1$2-$3$4#$3/
/ξ(\w.*)(\w.*)-(-+)(\w.*)#\3$/$1$2#$3$4-$3/
/^(\w.*)#(\w.*)-(\w.*)$/ξ$2#$3$1-/
/ξ//!

Regeln 0 oder 1 wechseln sich mit Regel 2 ab. Regel 2 dient dazu, die kleinste Scheibe eins weiterzugeben (mod 3). Regel 0 resp. Regel 1 führen geweils den einzigen legalen Zug, der die kleinste Scheibe nicht betrifft, aus.

8 Vokalen und Konsonantentrenner

Erstelle einen Algorithmus, der die Buchstaben in einem Text nach Vokalen und Konsonanten auftrennt.

Eingabe

guten morgen liebe sorgen

Ausgabe

Vokale      : ueoeieeoe
Konsonanten : gtnmrgnlbsrgn

Loading ⌛

Lösung

/ //g
/([^aeiou])([aeiou])/$2$1/g
/([aeiou]+)([^aeiou])/Vokale      : $1\nKonsonanten : $2/ !

9 Conway Folge

Problemstellung: Prüfe ob eine Zahl zur Conway-Folge 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, … gehört (✔) oder nicht (✘).
Beispiele: 111221→ 111221 ✔; 111222→ 111222 ✘
Idee: Erstelle beginnend mit 1 solange das Folgeelement der Conway-Folge bis dieses der Eingabe entspricht. Falls dabei ein Folgeelement länger als die Eingabe wird kann die Berechnung abgebrochen werden.
Da die Länge von Zeichenketten in Markov-Algorithmen nicht direkt verglichen werden kann, wird diese mit dem Hilfssysmbol : in unärer Schreibweise laufend ermittelt. 1211 → ::::1211 (entspricht der Textlänge 4)

Loading ⌛

Antwortzugng

/^1$/$& ✔/
/^\d+$/α1βγ$&/

/γ(\d)/:$1γ/
/(\d)(:+)/$2$1/g

/α(\d)\1\1/::3$1α/
/α(\d)\1/::2$1α/
/α(\d)/::1$1α/

/:+(\d+)αβ:+\1γ/$1 ✔/
/(:+):+.*β\1(\d+)γ/$2 ✘/
/:+(\d+)α/α$1/g

Erläuterungen

A Initialisierung: Die erste Regeln prüften den Trivialfall 1. Ansonsten kommt die zweite Regel zum Zug welche den eigentlichen Algorithmus initialisiert:
111221 → α1βγ111221
B Eingabelänge: Über Regel 4 und 5 werden solange : eingefügt und umplatziert bis die Länge der Eingabe unär feststeht. Dabei wandert γ ans Ende.
α1βγ111221 → α1β::::::111221γ
C Folgeelement: Es folgt über die Regeln 7 bis 9 die Bestimmung des Folgeelements und dessen unären Länge zwischen α und β. Dabei wandert α zu β.
α1β::::::111221γ → ::11αβ::::::111221γ
D Inhaltsvergleich: Über Regel 11 wird geprüft ob die beiden Elemente links von α und γ identisch sind und ein Element der Conwey-Folge konnte gefunden werden (STOP ✔):
::::::111221αβ::::::111221γ → 111221 ✔; Über Regel 12 prüft der Algorithmus ob das letzte berechnete Folgeelement bereits mehr Zeichen als die zu prüfende Eingabe hat (STOP ✘).
::::::::13112221αβ::::::111222γ → 111222 ✘; Über Regel 13 wird der nächste Iterationsschritt eingeleitet, so dass anschliessend das nächste Folgeelement berechnet werden kann (WEITER BEI C):
::::1211αβ::::::111221γ → α1211β::::::111221γ

exorciser.ch

Webseiten-Werkzeuge

Inhaltsverzeichnis

Aufgaben Serie C

1 X-Mas Tree

2 Pascalsche Dreieck

3 Häufigste Wort in einem Text

4 Zahlenreihe

5 Römische Zahlen II

6 Römische Zahlen III

7 Towers of Hanoi

Lösungen

8 Vokalen und Konsonantentrenner

9 Conway Folge

Erläuterungen

Benutzer-Werkzeuge

Seiten-Werkzeuge

Webseiten-Werkzeuge