📈 Zeitreihenvorhersage
🎯 In diesem Kapitel erfährst du, wie du mit neuronalen Netzen Zeitreihen vorhersagen kannst.
💡 Dieses Thema setzt Grundwissen bezüglich neuronaler Netze voraus (dieses Grundwissen wird z.B. in Künstliche Intelligenz für echte Fische vermittelt).
1. Einfache Zeitreihenvorhersage
Zeitreihe der stündlichen Messgrösse X. Horizontal sind die Tagesstunden ersichtlich, vertikal die Werte der Messgrösse X. Orange: beobachtete Vergangenheit, Grün: vorherzusagende Zukunft 1)
💡 Eine Zeitreihe vorherzusagen kann für vieles nützlich sein, z.B. eine Vorhersage von Wetter- oder Klimamesswerten, von Börsenkursen, Hochwasserständen etc.
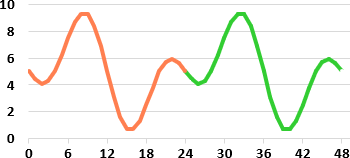
Im Folgenden betrachten wir die fiktive stündliche Zeitreihe der ominösen Messgrösse X, welche sich alle 24 Stunden wiederholt (siehe nebenstehende Abbildung). Wir nutzen ein neuronales Netz, um diese Zeitreihe zu lernen und zukünftige Werte vorherzusagen. Konkret soll das neuronale Netz mit den orangen Werten in der Abbildung trainiert werden und danach die „unbekannten“ grünen Werte möglichst genau vorhersagen.
Eine digitale Zeitreihe besteht aus mehreren einzelnen Messpunkten, welche normalerweise in gleichen zeitlichen Abständen voneinander aufgezeichnet wurden. Die untenstehenden Abbildungen zeigen dies im Detail.
🤔 Wie lässt sich nun eine solche digitale Zeitreihe vorhersagen?
💡 Eine einfache Idee ist z.B. die Folgende. Wir verwenden jeweils die letzten vier Werte der Zeitreihe als Eingangswerte für ein neuronales Netz (die letzten vier Werte können gemessen oder auch vorhergesagte Werte sein). Diese vier Werte sind in den Abbildungen dunkelblau eingezeichnet. Das neuronale Netz wird zuvor so trainiert, dass es immer nur den nächsten, unbekannten Wert voraussagt. D.h. das neuronale Netz sagt nur einen Zeitschritt (+1 Stunde) voraus. Dieser vorhergesagte Wert ist grün eingezeichnet. Ist ein grüner Wert berechnet worden, so kann auch dieser für die Vorhersage des nächsten Zeitschritts ebenfalls als Eingangswert für das neuronale Netz genommen werden. D.h. das neuronale Netz sagt einen Zeitpunkt voraus, rutscht eine Position weiter und sagt den nächsten Zeitpunkt voraus usw. (dies ist in den drei Abbildungen von links nach rechts ersichtlich).
 Zeitreihenvorhersage für Zeitschritt 342) |  Zeitreihenvorhersage für Zeitschritt 353) |  Zeitreihenvorhersage für Zeitschritt 364) |
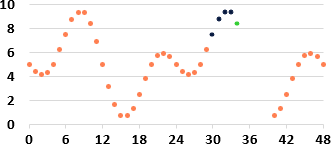
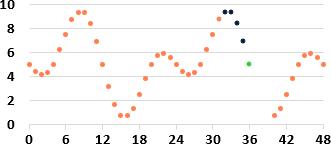
🤔 Wie kann ein neuronales Netz aber für so was trainiert werden?
💡 Im Prinzip genau gleich. Es werden jeweils vier nacheinander folgende Zeitpunkte der bereits bekannten Zeitreihe als Eingangswerte genommen und zusätzlich der nächste, fünfte Zeitpunkt als gewünschter Ausgangswert verwendet, der vorhergesagt werden sollte (Desired Output). Dafür muss der Wert dieses fünften Zeitpunkts natürlich bekannt sein. So kann das neuronale Netz lernen, welcher Wert jeweils nach vier Zeitpunkten als Nächstes kommt.
🤔 Und wie können wir sagen, wie gut die Vorhersage ist?
💡 Wir lassen das neuronale Netz eine Vorhersage für den nächsten Zeitpunkt (+1 Stunde) erstellen. Diesen vorhergesagten Wert nennen wir $v$. Da wir den richtigen Wert für die Vorhersage kennen (den Desired Output) können wir den Vorhersagewert $v$ mit dem richtigen, beobachteten Wert $b$ vergleichen.
Für uns spielen zwei Fehlermasse eine Rolle.
- Mean Absolute Error (MAE)
- Der Differenzbetrag $|v - b|$ zwischen vorhergesagten Wert $v$ und beobachteten Wert $b$ wird grösser, je mehr die beiden Werte voneinander abweichen. Um zu berechnen, wie gut eine Vorhersage ist, wird nicht nur eine Prognose durchgeführt, sondern viele verschiedene. Der Mittelwert der Differenzbeträge, der sogenannte Mean Absolute Error (MAE), beschreibt, wie nahe die Prognose der Wirklichkeit im Mittel kommt. Je kleiner der MAE, desto besser. Der MAE hat dieselbe Einheit wie der vorhergesagte Wert.
- Mean Squared Error (MSE)
- Das Differenzquadrat $(v - b)^2$ zwischen vorhergesagten Wert $v$ und beobachteten Wert $b$ wird grösser, je mehr die beiden Werte voneinander abweichen. Um zu berechnen, wie gut eine Vorhersage ist, wird nicht nur eine Prognose durchgeführt, sondern viele verschiedene. Der Mittelwert davon, der sogenannte Mean Squared Error (MSE) beschreibt, wie nahe die Prognose der Wirklichkeit im Mittel kommt. Je kleiner der MSE, desto besser.
⚠️ Für die Beschreibung dafür, wie gut eine Zeitreihe vorhergesagt wird, verwenden wir den MAE, da dieser, im Gegensatz zum MSE, dieselbe Einheit wie die Zeitreihe hat. So lässt sich z.B. für eine Temperaturprognose sagen, dass diese im Mittel 2 °C abweicht. Für das Training des neuronalen Netzes verwenden wir den MSE, da dieser grosse Abweichungen zwischen vorhergesagten Wert $v$ und beobachteten Wert $b$ während des Trainings aufgrund des Quadrats stärker bestraft als der MAE (je grösser der Fehlerwert, desto grösser die Anpassung der Gewichte).
✍ Auftrag 1 – Teil 1
Hier trainierst du ein neuronales Netz, welches die Zeitreihe genau +1 Stunde in die Zukunft vorhersagt. Sobald das neuronale Netz trainiert ist, sagst du +1 Stunde voraus, verwendest die +1 Stundenprognose um, wie oben gezeigt, eine +2 Stundenprognose zu erzeugen etc. bis eine Prognose bis +120 Stunden in die Zukunft entsteht.
- Starte das untenstehende Programm und studiere die folgenden Punkte (es dauert einen kleinen Moment, bis die Zeitreihe angezeigt wird).
- Während dem Training wird der Trainingsfehler „loss“ (MSE für die +1 Stundenprognose) angezeigt.
- Danach wird eine Grafik für eine Prognosezeitreihe ausgehend von einem Startpunkt erzeugt mit
- der wahren, beobachteten Zeitreihe (orange)
- der vorhergesagten Zeitreihe (grün)
- Zusätzlich wird der MAE für die +1, +2, +3, … + 120 Stundenprognosen (violett) berechnet. Der MAE wird über mehrere Prognosenzeitreihen ausgehend von mehreren, verschiedenen Startpunkten aus gemittelt.
- Du kannst nach dem Training zwischen einer Beschreibung des neuronalen Netzes, dem Trainingsfehler und der Vorhersage über die Register
Modell,TrainingundResultathin und her wechseln.
- Notiere den MAE für die +72 Stundenprognose, fahre dazu einfach mit der Maus auf die Grafik und suche den MAE für
x = 72. Loading ⌛ - Starte das Training noch zwei weitere Male und falls du einen tieferen MAE für die +72 Stundenprognose erzielst, so überschreibe damit den MAE Wert im obigen Textfeld.
- Warum wird der MAE tentenziell immer grösser mit fortschreitender Prognosezeit? Schreibe deine Vermutung in das Textfeld. Loading ⌛
- Vergleiche deine Antwort mit unserer Antwort
✍ Auftrag 1 – Teil 2
- Ändere in der ersten Sektion im obigen Programmcode die Parameter ab und wiederhole das Training ein paar Male mit verschiedenen Einstellungen. Die Parameter sind die Folgenden:
TIMESERIES_FEATURES: Bestimmt, wie viele vergangene Zeitpunkte als Eingangsgrössen verwendet werden. In den einleitenden Grafiken werden vier vergangene Zeitpunkte verwendet (die dunkelblauen Punkte).LERNRATE: Legt fest, wie stark sich die Gewichte des neuronalen Netzes pro Schritt ändern dürfen. Ist der Wert zu hoch, springt der Fehler (loss) während des Trainings hin und her, ist der Wert zu tief, brauchst du viel Geduld…
⚠️ Achtung! Bei einer viel zu hohen Lernrate kann es sogar sein, dass das neuronale Netz derart stark springt, dass die Zahlen grösser werden, als der Computer diese anzeigen kann. Dann wird keine grüne Linie gezeichnet und als Loss „NaN“ (not a number) ausgegeben. Dann ist einfach eine kleinere Lernrate zu wählen.ANZAHL_HIDDEN_NEURONS: Bestimmt die Komplexität des neuronalen Netzes. Ist der Wert zu hoch, kann Overfitting auftreten (was für dieses Beispiel, weniger ein Problem darstellt), ist die Zahl zu klein, kann die Zeitreihe nicht genügend vorhergesagt werden.ANZAHL_EPOCHEN: Legt die Anzahl der „Lerndurchgänge“ fest. Je grösser dieser Wert ist, desto länger wird trainiert.
- Notiere, mit welchen Parametereinstellungen du den tiefsten MAE für die +72 Stundenprognose erzielen konntest. Loading ⌛
2. Fachwissen einbauen
🤔 Vermutlich waren deine Zeitreihenvorhersagen im vorangehenden Auftrag nicht ganz perfekt oder du musstest viele Eingangsgrössen (input features) verwenden.
⚠️ Für die Wahl der Eingangsgrössen ist es immer eine gute Idee, Fachwissen, d.h. Wissen über die zu vorhersagende Grösse, zu berücksichtigen. Interessant ist, dass sich die Zeitreihe alle 24 Stunden wiederholt.
💡 Also bauen wir die Tagesstunde 0 - 23 als zusätzliche Eingangsgrösse mit ein (24 Uhr wäre ja wieder 0 Uhr).
✍ Auftrag 2
Im nachfolgenden neuronalen Netz ist die Tagesstunde als zusätzliche Eingangsgrösse mit eingebaut. Bei der Wahl TIMESERIES_FEATURES = 12 besitzt das neuronale Netz daher 13 Eingangsgrössen.
- Starte wiederum das Programm zwei, dreimal und halte die tiefste MAE bei einer Prognosezeit von +72 h fest.Loading ⌛
- Verglichen mit dem MAE in „Auftrag 1 - Teil 1“ ist das Resultat besser oder schlechter?Loading ⌛
- Wenn du das Programm mehrfach startest, sind die Resultate in etwa gleich gut oder stellst du grössere Unterschiede fest?
3. Dem neuronalen Netzwerk helfen
🤔 Vermutlich hast du festgestellt, dass das neuronale Netz in „Auftrag 2“ manchmal besser und manchmal schlechter abschneidet als das neuronale Netz in „Auftrag 1 - Teil 1“, obwohl es eine Eingangsgrösse mehr besitzt. Es erscheint fast so, als würde die neue Eingangsgrösse das neuronale Netz manchmal „verwirren“.
⚠️ Das Problem ist der Sprung in der Stundenangabe (siehe unten). Für das neuronale Netz ist der Minimalwert 0 Uhr und der Maximalwert 23 etwas komplett anderes. Für uns (und in der Zeitreihe) sind 0 Uhr und 23 Uhr fast dasselbe.
Dunkelblau: Tagesstunde5)
🤔 Aber wie können wir 24 Stunden mit einer Zahl so darstellen, dass es keinen Sprung gibt, jedoch jede Tagesstunde einen anderen Wert bekommt?
💡 Bevor du dir den Kopf zerbrichst, das ist mit einer Zahl nicht möglich, jedoch mit zwei Zahlen schon! Die Idee besteht darin, die Tagesstunde durch den Sinus UND den Cosinus der Tagesstunde zu ersetzen, d.h. durch zwei Eingangsgrössen.6). So wird jede Tagesstunde durch ein anderes Sinus / Cosinus Wertepaar dargestellt (siehe unten).
Dunkelblau: Tagesstunde; Blaugrau: Sinus der Tagesstunde; Grau: Cosinus der Tagesstunde7)
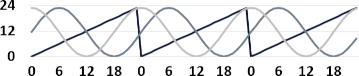
💡 Also bauen wir statt der Tagesstunde, die Sinus- und Cosinuswerte der Tagesstunde als zusätzliche Eingangsgrössen mit ein.
✍ Auftrag 3
Neben vergangenen Werten der Zeitreihe werden hier zusätzlich Sinus und Cosinus der Tagesstunde verwendet. Bei der Wahl TIMESERIES_FEATURES = 12 besitzt das neuronale Netz somit 14 Eingangsgrössen.
- Starte das Programm. Ist das Resultat nun besser oder schlechter in den vorangehenden Aufträgen? Loading ⌛
- Spiele mit den Parametern etwas herum. Mit wie weinigen
TIMESERIES_FEATURESbekommst du eine MAE für die +72 Stundenprognose von weniger als 0.1 hin? Halte die MAE zusammen mit deiner neuronalen Netz Einstellung im Textfeld fest. Loading ⌛
4. Technisches Wissen nutzen
🙂 So weit, so gut, du konntest dank Fachwissen (dem Einbauen von Sinus und Cosinus der Tagesstunde) bereits mit relativ wenigen Eingangsgrössen gute Resultate erzielen.
🤔 Wie sieht es aber mit technischem Wissen aus? Kann das dir noch weiter helfen?
💡 Die obigen neuronalen Netze waren „Old School“ aufgebaut. D.h. es wurden relativ wenige Hidden Neuronen verwendet, dafür waren die einzelnen Hidden Neuronen relativ komplex aufgebaut8) und für das Training wurde seit längerem bewährter Lernalgorithmus verwendet9). Das nachfolgende Programm nutzt ein neuronales Netzwerk, das gemäss einer neueren „Deep Learning“-Philosophie aufgebaut wurde. D.h. es nutzt nicht nur eine, sondern zwei Schichten Hidden Neuronen (und somit auch mehr Hidden Neuronen), aber dafür einfacher aufgebaute Hidden Neuronen 10) und für das Training wird ein modernerer, aggressiverer Lernalgorithmus verwendet, welcher ohne Lernrate auskommt 11).
✍ Auftrag 4
In der Defaulteinstellung nutzt das neuronale Netz nur einen einzigen vergangenen Wert der Zeitreihe sowie Cosinus und Sinus der Tagesstunde, d.h. nur 3 Eingangsgrössen.
- Starte das Programm zwei oder dreimal. Ist das Resultat nun besser oder schlechter in den vorangehenden Aufträgen? Wie vergleicht sich das hier genutzte neuronale Netz mit den zuvor genutzten neuronalen Netzen? Loading ⌛
5. 🤩 Auf der Suche nach einer Herausforderung
🤩 Kapitel für Schnelle oder Interessierte
Das neuronale Netz in „Auftrag 4“ ist so gut, dass es sich kaum lohnt, Parameter anzupassen. In diesem Abschnitt wird die Aufgabe für das „moderne“ neuronale Netz aus „Auftrag 4“ etwas erschwert, indem die Tagesstunde nicht mehr als Eingangsgrösse verwendet wird.
<WRAP center round box>
Auftrag 5
Das neuronale Netz verwendet ausschliesslich vergangene Werte der Zeitreihe als Eingangsgrössen. Obwohl der verwendete Lernalgorithmus ohne Lernrate auskommt, kann dieser in diesem Auftrag zusätzlich mit einer Lernrate „getuned“ werden.
- Starte das Programm zwei oder dreimal. Spiele mit Parametern etwas herum. Versuche, mit möglichst wenigen
TIMESERIES_FEATURESauszukommen. Halte fest, mit welchen Einstellungen du dein bestes Resultat erzielen konntest.Loading ⌛
Eigene Notizen
Loading ⌛
6)
Genauer gesagt verwenden wir
sin(2*π*hour/24) und cos(2*π*hour/24) als zusätzliche Eingangsgrössen. Das 2*π/24 sorgt dafür, dass der Sinus und der Cosinus nach 24 Stunden wieder die Anfangswerte einnimmt.8)
Es wurde die komplexe „Tangens hyperbolicus“-Funktion in den Neuronen eingesetzt.
9)
Es wurde der klassische „Backpropagation“-Algorithmus genutzt.
10)
Es werden die einfach zu berechnende „ReLU“-Funktion in den Neuronen eingesetzt.
11)
Es wird der populäre „Adam“-Algorithmus genutzt.